<La Comunidad-Hacker> - Que es un Algoritmo ( Resumido)

Algoritmos

Un algoritmo es una serie de pasos lógicos, que se estructuran para resolver un problema.
Generalmente un algoritmo se compone de sentencias simples y sentencias de control.

Los algoritmos están delimitados por la palabras : INICIO y FIN

Sentencias simples

Asignación de variables

Se le asigna un valor a una variable, a través del simbolo de flecha(<--) que dice que el valor a la derecha tiene que ser asignado a la variable que está a la izquierda.

ej:

a <-- 10

Se asigna un valor 10 a la variable a. Al escribir esta sentencia por primera vez en un algoritmo, da por entendido su declaración o creación.

Comunmente al lado derecho de la flecha, se pueden realizar operaciones aritméticas (+,-,/,*), para que su resultado se le asigne a la variable. Además en estas operaciones se puede incluir la misma variable u otras.

ejemplo :

INICIO

x <-- 5

y <-- 10

z <-- x + y

z <-- y * x + 7

z <-- x/8 + y/9 + (7 + x/8)

z <-- z + 1

z <-- z * z + y * y

x <-- -x + -y + -3
FIN

Ejemplo : determinar cuánto vale (a,b,c) después de las siguientes sentencias de asignación

INICIO
a <-- 2
b <-- a * 4 /* b <-- 2 * 4 = 8 */
a <-- b + 2 * a /* a <-- 8 + 2 * 2 = 12 */
b <-- 2 - a * b /* b <-- 2 - 12 * 8 = 2 - 96 = -94 */
a <-- a - b /* a <-- 12 - -94 = 12 + 94 = 106 */
b <-- -b + 6 /* b <-- --94 + 6 = 94 + 6 = 100 */
FIN

Para seguir en forma ordenada, el cambio de valores en las variables, se utiliza una tabla llamada traza.

a 2
---------------
b

a 2
---------------
b 8

a 2 12
---------------
b 8

a 2 12
---------------
b 8 -94

a 2 12 106
----------------
b 8 -94 100

valores finales : a = 106 , b = 100

Por lo tanto si se pide una traza, se debe mostrar la última tabla. Los pasos anteriores son sólo pasos explicativos.

ejercicio : hacer la traza del siguiente algoritmo

INICIO
t <-- 1
p <-- 4
t <-- 3 * t
p <-- p - 12
t <-- -t + 6
p <-- -p * -2
FIN

valores finales : t = 3 y p = -16

Lectura de variables
En muchos algoritmos, el valor de alguna variable debe ser introducido dinámicamente por el usuario a través del teclado o algún otro medio. A esa acción le llamaremos "leer", que consiste en la asignación del valor de entrada, a la variable correspondiente.

ejemplo:

INICIO
a <-- 12
leer b
a <-- a + b
FIN

Si se tiene que leer más de una variable, se pueden escribir usando el separado coma.

Ej : Leer a, b, c /* lee en ese orden las variables a, b y c */

Declaración de una constante

Si se necesita incluir en el algoritmo alguna constante, se debe seguir la misma metodología de la asignación de variables, pero con la limitación que el identificador debe estar escrito con letras mayúsculas y que la declaración se haga a continuación del inicio del algoritmo.

Comentarios

Todo comentario de alguna sentencia, debe ir entre los simbolos /* */.
Los comentarios son útiles para explicar mejor alguna sentencia que puede estar no clara, para alguien que se enfrenta a las sentencias por primera vez.

Ej :

INICIO
PI <-- 3.14 /* constante */
Leer radio
area <-- 4 * PI * radio * radio /* area de una esfera */
FIN

Comparaciones

Para comparar dos variables se usará la siguiente nomenclatura :

a < b /* esta sentencia es verdadera (true) si a es menor que b, y es falsa (false) en caso contrario */
a > b /* esta sentencia es verdadera (true) si a es mayor que b , y es falsa (false) en caso contrario */
a <= b /* esta sentencia es verdadera (true) si a es menor o igual que b, y ees falsa " " */
a >= b /* esta sentencia es verdadera (true) si a es mayor o igual que b , y es falsa " " */
a == b /* esta sentencia es verdadera si a tiene el mismo valor de b, y es falsa en caso contrario */
a != b /* esta sentencia es verdadera si a no tiene el mismo valor de b, y es falsa en caso contrario */

Método imprimir

Se usara un método llamado "imprimir", para identificar una salida estándar (ej : pantalla o consola).

El método consiste de la palabra "imprimir", seguido de un conjunto de argumentos, delimitado entre paréntesis.

imprimir(..argumentos..)

Los argumentos pueden ser de dos tipos : constantes alfanuméricas o variables. Si se quiere encadenar una constante con una variable, se debe usar el separador '+'.

Ej:

INICIO
imprimir("Ingrese radio : "

/* imprime el mensaje constante "Ingrese x : " */
leer radio
imprimir("El valor del radio ingresado es : " + radio) /* se encadena lo constante con lo variable */
imprimir(r * 2) /* imprime el resultado de la operación aritmética */
FIN

En el caso que la operación tenga el operador suma, se deben adicionar paréntesis para su correcta interpretación. Debe ser interpretado como un operador aritmético y no de concatenación.

imprimir("la suma de a y b es : " + (a + b) )

imprimir("a + b + c +++"

/* como el simbolo suma esta dentro de la cadena constante, limitada
por comillas "", es interpretado como caracter */

SENTENCIAS DE CONTROL

SENTENCIA SI

SI (condicion) ENTONCES
sentencia_1
sentencia_2
:
sentencia_n
FIN SI

Si la condición es verdadera, entonces se ejecutarán en orden las sentencias delimitadas por el FIN SI.
Si la condición es falsa o no se cumple, el punto de algoritmo ejecutará la sentencia posterior al FIN SI.

Ejemplo : Una vez leidos b y c, si c es mayor que b, entonces asignar a b el valor de c y a continuación asignar a c el valor del doble de b.

INICIO

leer b
leer c

SI (c > b) ENTONCES
b <-- c
c <-- 2 * b
FIN SI
FIN

Ejemplo : Si a es igual a b, entonces imprimir "Diferencia cero". A continuación imprimir "Concluida la comparación"

INICIO
leer b,c
SI (c == b) ENTONCES
imprimir("Diferencia cero"

FIN SI
imprimir("Concluida la comparación"

FIN

EN GENERAL : Es válido, ejecutar un conjunto de sentencias de control, dentro de otra del mismo tipo.
Para una ordenada notación, todas las sentencias contenidas dentro de otra sentencia, se escribiran dejando un número positivo (recomendado : 4) de espacios a la derecha, de la columna correspondiente al inicio de la sentencia.

Para el caso de la sentencia SI, a continuación se muestra una abertura del ciclo de segundo orden :

INICIO
SI (c + a > 0 ) ENTONCES
imprimir("c + a es mayor que cero"

SI (c - a > 0) ENTONCES
imprimir("a es menor que c );
FIN SI
FIN SI
FIN

SENTENCIA SI - SINO

SI (condicion) ENTONCES
sentencia(s)
SINO
sentencia(s)
FIN SI

Si la condición es verdadera, entonces se ejecutarán las sentencias anteriores al SINO.
Si la condición es falsa, el punto de algoritmo ejecutará las sentencias posteriores al SINO.

Ejemplo :

SI (a != b) ENTONCES
imprimir("a es distinto de b"

SINO
imprimir("a es igual b "

FIN SI

SENTENCIA DE SELECCIÓN

SELECCION (variable)

constante_1 : sentencia(s)
constante_2 : sentencia(s)
:
:
constante_n : sentencia(s)
FIN SELECCION

Para eliminar el problema de tener muchas condiciones "SI (variable == valor_i) ENTONCES", se agrupan las instrucciones, en función del valor que tome cierta variable.

Ejemplo :

Algoritmo de la Calculadora

INICIO
imprimir("1.- suma"

;
imprimir("2.- resta"

;
imprimir("3.- multiplicacion"

imprimir("4.- division"

imprimir("Ingrese opcion : "

Leer a,b,opcion

SELECCION(opcion)

1 : imprimir("suma de " + a + " y " + b + " igual a : " + (a + b))

2 : imprimir("resta de " + a + " y " + b + " igual a : " + (a - b))

3 : imprimir("multiplicacion de " + a + " y " + b + " igual a : " + (a * b))

4 : SI (b != 0) ENTONCES
imprimir("division de " + a + " y " + b + " igual a : " + (a / b))
SINO
imprimir("division por cero --> infinito "

FIN SI

FIN SELECCION
FIN

CICLOS ITERATIVOS

SENTENCIA MIENTRAS

MIENTRAS (condicion) HACER
sentencia(s)
FIN MIENTRAS

Mientras se cumpla la condición, se ejecutarán las sentencias anteriores al FIN MIENTRAS. Además se cumple, que se puede entrar al ciclo, sólo si se cumple la condición. Finalmente, es muy importante determinar la variación de alguna variable, para quebrar la condición y no convertir al ciclo iterativo, en un "loop" o ciclo infinito.

Ej : Cantidad de dígitos de un número

INICIO

Leer numero
contador <-- 0

MIENTRAS (numero > 0) HACER
numero <-- numero / 10
contador <-- contador + 1
FIN MIENTRAS

imprimir("cantidad de digitos : " + contador)
FIN

SENTENCIA HACER MIENTRAS

HACER
sentencia(s)
MIENTRAS (condición)

Se ejecutarán las sentencias, mientras se cumpla la condición. Además, una diferencia con la sentencia de control anterior, es que en ésta por lo menos se entra una vez en el ciclo.

Ej : leer un carácter, mientras sea distinto de '#'

INICIO
HACER
leer caracter
MIENTRAS (caracter != '#')
FIN

SENTENCIA PARA

PARA variable <-- valorInicial HASTA valorFinal HACER
sentencia(s)
FIN PARA

Esta sentencia es útil para hacer variar el valor de una variable entera, permitiendo su inicialización y la determinación del último valor que puede tomar dentro del ciclo.

El ciclo cumple los siguientes pasos :

1) Inicializa el valor de la variable
2) Revisa la condición de término
3) SI se cumple la condición ENTONCES
ejecuta la sentencia
incrementa la variable
Vuelve al paso 2)
SINO saltar al paso 4)
4) Fin del ciclo

Ejemplo :

1) Imprimir todos los dígitos (0..9)

PARA i <-- 0 HASTA 9 HACER
imprimir(i)
FIN PARA

PROBLEMAS RESUELTOS

Problema del triángulo

Determinar si un triangulo es : equilatero, isóceles o escaleno, conociendo sus tres lados (a,b,c).

INICIO
leer a,b,c
SI (a == b) ENTONCES
SI (b == c) ENTONCES
imprimir("Triangulo Equilátero"

SINO
imprimir("Triangulo Isóceles"

FIN SI
SINO
SI (b == c) ENTONCES
imprimir("Triangulo Isóceles"

SINO
imprimir("Triangulo Escaleno"

FIN SI
FIN SI
FIN

Problema del fósforo, el ventilador y la vela

Def : encender una vela con un fósforo, en función con las siguientes restricciones.

Existe un ventilador que se ubica frente al camino del fósforo prendido, el cual genera una corriente de aire, que se interpone a la llegada del fósforo prendido. Se cuenta con una cantidad limitada de fósforos, que se deben gastar completamente si es que no se lográra prender la vela. El ventilador no se puede apagar durante los intentos.

Variables

n : Número inicial de fósforos.

f : número de fósforos quemados. Por cada ensayo fallido, esta variable disminuirá en
una unidad. Posibles valores : {n , n - 1 , n -2 , .. , 1 , 0 }.

velaApagada : estado lógico {true,false}

Métodos

intento() : retorna true si la vela fue prendida, retorna false en caso que la vela siga apagada.

imprimir() : imprime según los parámetros.

Una vez que se prende, mostrar o imprimr la cantidad de fósforos quemados y sin usar. Si no se prende nunca, imprimir el mensaje : "no se pudo prender la vela."

INICIO

Leer n
velaPrendida <-- false

f <-- 0

SI (velaPrendida == false) ENTONCES
MIENTRAS (n - f > 0) HACER
f <-- f + 1 /* aumento en 1, los fosforos usados */
velaPrendida <-- intento() /* la variable puede tomar valor true o false */

SI (velaPrendida == true)
imprimir("Cantidad de fosforos quemados :" + f )
imprimir("Cantidad de fosforos sin usar :" + (n - f) )
f <-- n /* se fuerza a salir del ciclo mientras, quebrando su condición */
FIN SI
FIN MIENTRAS
SINO
imprimir("No se pudo prender la vela"

FIN SI

FIN

Problema del reconocimiento de cadena en un proceso de transición de estados

Un proceso computacional, lee una cadena constante formada por ceros y unos (terminada en "#"

("0110#" , "11000110#",...) para verificar su reconocimiento o no.
El proceso reconoce una cadena, si es que al terminar de leer ésta (leer caracter "#"

, el proceso se encuentra en el estado c.

Especificaciones del proceso

1) El proceso parte en el estado a y lee el primer carácter de la cadena.

2) Si el proceso está en el estado a y es leído un carácter "1" entonces el estado del proceso cambia a b. En caso contrario si es que el carácter leído es un "0", el estado se mantiene en a.

3) Si el proceso está en el estado b y si lee un carácter "1" el proceso se mantiene en el mismo estado. En caso contrario, si el carácter leído es un "0" el estado cambiará a c.

4) Si el proceso está en el estado c y es leído un carácter "1" el proceso cambia al estado a. En caso contrario, si el carácter leído es un "0" el estado se mantiene en c.

5) La cadena no puede comenzar con el carácter "#".

Cadenas que dejan el proceso en estado A : {"0#" , "00#" ,.., "101#" , "0101#" , "00101101#" ,...}

Cadenas que dejan el proceso en estado B : {"1#" , "01#" ,.., "111#" , "0011#" , "01101011#" ,...}

Cadenas que dejan el proceso en estado C : {"10#" , "010#" ,.., "001100#" , "101100110#" , ...}

Se pide diseñar un algoritmo que lea una cadena (String) y determine el estado del proceso en función de aquella.
Además, si la cadena de entrada deja al proceso en el estado c, ésta se deberá imprimir, en caso contrario se deberá imprimir "cadena no reconocida".

Algoritmo

INICIO
estado <-- a
leer cadena

c <-- leerCaracter()
HACER
SELECCION(estado)
a : SI (c == 1) ENTONCES
estado <-- b
FIN SI
b : SI (c == 0) ENTONCES
estado <-- c
FIN SI
c : SI (c == 1) ENTONCES
estado <-- a
FIN SI
FIN SELECCION

c <-- leerCaracter()

MIENTRAS (c != "#"

SI (estado == c) ENTONCES
imprimir(cadena)
SINO
imprimir("cadena no reconocida"

FIN SI
FIN

Problema de detención en un semáforo

Escribir el algoritmo, que describe las acciones que el conductor realiza ante el estado verde,amarillo o rojo de un semáforo. Tener en cuenta, que ante una luz amarilla, el conductor acelerará si es arriesgado, o desacelerará si es que es prudente.

Variables

luz : {VERDE , AMARILLA , ROJA}
estaDetenido : {true,false}

Métodos

parte() , pasa() , acelera() , desacelera(), frena(), estaDetenido(), espera()

INICIO
leer luz

SELECCION (luz)

VERDE : SI (estaDetenido == false) ENTONCES
parte()
SINO
pasa()
FIN SI

AMARILLA : SI (conductorEsArriesgado == true) ENTONCES
acelerarara()
SINO
desacelera()
frena()
FIN SI

ROJA : SI (estaDetenido == false) ENTONCES
desacelera()
frena()
SINO
espera()
FIN SI

FIN SELECCION

FIN

Problema de compra en función de la calidad de un lote de productos

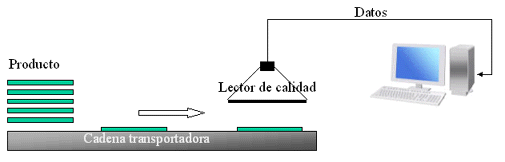
Se requiere implementar un algoritmo, que permita registrar la calidad de un lote de productos, para agilizar el proceso de compra.

El sistema consiste, en un lector de calidad que va leyendo mediante sensores a un producto dejado a través de una correa transportadora, para transmitir a continuación los datos a un software especial, depositado en un computador, que entrega hacia afuera uno de los siguientes estados numéricos :

0 : Producto MALO
1 : Producto DEFECTUOSO
2 : Producto BUENO

Especificaciones

a) Los datos que llegan en forma iterativa (mientras no se haya acabado el lote de productos a revisar), son rescatados por el método test().

b) El térnmino de la revisión está determinado cuando el método fin() retorne el valor true.

c) El algoritmo debe llevar un conteo de cuántos productos corresponden a cada
estado { MALO : 2 , DEFECTUOSO : 5 , BUENO : 43 }, para posteriormente aplicar un cálculo de porcentaje.

d) Inicialmente no se sabe la cantidad total de productos del lote, por lo tanto es fundamental que se implemente un contador para los cálculos posteriores.

e) El precio original de compra del lote, tiene que ser ingresado por el usuario. Después del análisis, se deberá imprimir según los criterios el precio propuesto de compra.

Una vez terminado el proceso de análisis y conteo, se determinará el precio de compra propuesto para el lote en cuestión.

Criterios

1) Si el porcentaje de productos malos es superior al 15%, el lote no se compra (precio <-- 0). En caso contrario, pasar al punto 2)

2) Si el porcentaje de productos defectuosos es menor a un 10%, se compra a un 70% del precio original. En caso contrario, pasar al punto 3)

3) Si el porcentaje de productos buenos es mayor o igual a un 70%, el lote se compra al precio original. En caso contrario, se estaría comprando a un 60% del precio original.

Algoritmo

INICIO
N <-- 0 /* cantidad de productos analizados */
contMalos <-- 0
contDefect <-- 0
contBuenos <-- 0
precio <-- 0 /* precio en función del análisis */

leer precioInicial

MIENTRAS (fin() != true) HACER

calidad <-- test()

SELECCION (calidad)

0 : contMalos <-- contMalos + 1
1 : contDefect <-- contDefect + 1
2 : contBuenos <-- contBuenos + 1

FIN SELECCION

N <-- N + 1

FIN MIENTRAS

SI (contMalos / N > 0.15) ENTONCES
precio <-- 0
SINO
SI (contDefect / N < 0.1 ) ENTONCES
precio <-- precioInicial * 0.7
SINO
SI (contBuenos / N >= 0.7 ) ENTONCES
precio <-- precioOriginal
SINO
precio <-- precioOriginal * 0.6
FIN SI
FIN SI
FIN SI

imprimir(precio)

FIN

Problemas resueltos y una pequeño vistazo al lenguaje Java

Problema de los trampolines

Se cuenta con dos trampolines olímpicos, para que una persona pueda realizar una serie de saltos, con tal de terminar parado en el segundo trampolín.
La distancia vertical entre los trampolines, es de 3 metros. Se sabe que siempre el primer salto es de 60 cm (0,6 mts).
Además, se sabe que en cada salto se supera el rendimiento del salto anterior en un 30%.

Determinar : cantidad de saltos necesarios para alcanzar el segundo trampolín y la altura máxima que se llega con respecto al primer trampolín. Además se necesita saber la altura alcanzada en cada salto.

ejemplo :

separación entre trampolines : 3.0
porcentaje de aumento (0..1) : 0.3

cs altura
-- ------
1 0.6
2 0.78
3 1.014
4 1.3182
5 1.7137
6 2.2278
7 2.8961

Cantidad de saltos : 8
Altura maxima alcanzada : 3.765

seguir(1)/salir(0) : 0

Algoritmo

INICIO
cs <-- 1 /* cantidad de saltos */
h <-- 0.60 /* altura */

MIENTRAS( h < 3.0 ) HACER
cs <-- cs + 1
h <-- h * 1.3
FIN MIENTRAS

imprimir("Cantidad de saltos : " + cs)
imprimir("Altura maxima alcanzada : " + h)
FIN

Programa en Java

import java.io.*;

public class Trampolin {
public static void main(String[ ] args) throws IOException {

int cs = 1;
double h = 0.60;
int seguir = 1;
double sep,aumento;

BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

do {

h = 0.6;
cs = 1;

System.out.print("nnseparacion entre trampolines : "

;
sep = Double.parseDouble(in.readLine());

System.out.print("porcentaje de aumento (0..1) : "

;
aumento = Double.parseDouble(in.readLine());

aumento += 1.0;

System.out.println("ntcstaltura"

;
System.out.println("t--t------"

;

while ( h < sep ) {

System.out.println("t" + cs + "t" + h);

cs++;
h *= aumento;
}

System.out.println("ntCantidad de saltos : " + cs);
System.out.println("tAltura maxima alcanzada : " + h);

System.out.print("nttseguir(1)/salir(0) : "

;
seguir = Integer.parseInt(in.readLine());

} while (seguir == 1);
}
}

Bajar archivo

Problema del electrón en los anillos

a ) Un electrón se mueve en un conjunto de 10 anillos, con una velocidad constante en cada uno de ellos . Una caracteristica de la trayectoria, es que una vez que completa el recorrido en un anillo, cambia de estado pasándose al anillo siguiente o más cercano al centro, con una velocidad 1.12 veces mayor a la anterior.

El electrón, después de recorrer el último anillo y llegar teóricamente al centro (k = 0), sale disparado perpendicularmente al radio del anillo, a una velocidad igual al doble de velocidad del radio uno (k = 1) por el último radio al cuadrado.

Además, la trayectoria cuenta con la caracteristica que el radio de cada anillo, es un 35% menor con respecto al anterior, siendo el radio inicial de 5.0 nm.

Finalmente, se sabe que el electrón tiene una velocidad inicial de 2.0 ns.

Datos

Para k : 1 , ... , 10 se tiene que

radio de cada anillo : radio_k-1 = radio_k * 0.65

Velocidad constante en cada anillo : v_k-1 = 1.12 * v_k

Tiempo_k = Distancia_k / Velocidad_k

radio inicial = 5.0 [nm]

velocidad disparo = 2 * v_1 * (1 + radio)^2

Determinar

Velocidad, distancia y tiempo en recorrer cada anillo, además del tiempo acumulado para recorrer los 10 anillos y la velocidad de disparo del electrón.

El algoritmo debe generar la siguiente salida :

ingrese numero de anillos : 10
ingrese radio inicial : 5.0
ingrese velocidad inicial : 2.0

k radio Distancia Velocidad Tiempo
--- ----- --------- --------- ------
10 5.0 31.415 2.0 15.707963267948966
9 3.25 20.42 2.24 9.11622868229181
8 2.112 13.273 2.508 5.2906684316872115
7 1.373 8.627 2.809 3.07047721481847
6 0.892 5.607 3.147 1.781973383600005
5 0.58 3.645 3.524 1.0341809815535743
4 0.377 2.369 3.947 0.6001943196516281
3 0.245 1.54 4.421 0.3483270605121055
2 0.159 1.001 4.951 0.20215409761863268
1 0.103 0.65 5.546 0.11732157451081357

Velocidad disparo : 14.152
tiempo total : 37.26948901419321

Algoritmo

INICIO

PI <-- 3.14 /* constante */
k <-- 10
radio <-- 5.0
velocidad <-- 2.0
distancia <-- 0
tiempo <-- 0
tiempoAcum <-- 0

imprimir("k radio Distancia Velocidad Tiempo"

;
imprimir("----------------------------------------------"

;

MIENTRAS (k > 0) HACER

distancia <-- 2 * PI * radio
tiempo <-- distancia / velocidad
tiempoAcum <-- tiempoAcum + tiempo
imprimir(k + " " + radio + " " + distancia + " " + Velocidad" + " " + tiempo)
velocidad <-- 1.12 * velocidad
radio <-- radio * 0.65

k <-- k - 1

FIN MIENTRAS

velocidad <-- 2 * velocidad * (1 + radio) * (1 + radio)

imprimir("Velocidad disparo : " + velocidad)
imprimir("tiempo total : " + tiempoAcum)

FIN

b ) Realizar un algoritmo en donde la cantidad de anillos, el radio inicial y la velocidad inicial, sean variables que deben ser leídas. Además, se quiere permitir tener la opción de salir o seguir calculando con nuevos valores.

Solución

INICIO

PI <-- 3.14 /* constante */
distancia <-- 0
tiempo <-- 0
seguir <-- 1

HACER

tiempoAcum <-- 0 /* en cada ciclo se debe inicializar en cero */
imprimir("ingrese numero de anillos : "

leer k
imprimir("ingrese radio inicial"

leer radio
imprimir("ingrese velocidad inicial"

leer velocidad imprimir("k radio Distancia Velocidad Tiempo"

;
imprimir("----------------------------------------------"

leer seguir

MIENTRAS (seguir == 1)
FIN

Programa en Java
import java.io.*;

public class Anillo {

private static double redondear(double num) {
double aux = num * 1000;
int tmp = (int) aux;
return (double) tmp / 1000;
}

public static void main(String[ ] args) throws IOException {
double distancia = 0.0;
double tiempo = 0.0;
double tiempoAcum = 0.0;
double radio;
int k;
double velocidad;
int seguir = 1;

BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

do {

tiempoAcum = 0.0; /* en vcada ciclo se debe inicializar en cero */

System.out.print("nningrese numero de anillos : "

;
k = Integer.parseInt(in.readLine());

System.out.print("ingrese radio inicial : "

;
radio = Double.parseDouble(in.readLine());

System.out.print("ingrese velocidad inicial : "

;
velocidad = Double.parseDouble(in.readLine());
System.out.println("nnktradiottDistanciatVelocidadtTiempo"

;
System.out.println("---t-----tt---------t---------t------"

;

while (k > 0) {

distancia = 2.0 * Math.PI * radio;

tiempo = distancia / velocidad;

tiempoAcum = tiempoAcum + tiempo;

System.out.println(k + "t" + redondear(radio) + "tt" + redondear(distancia) + "tt" +
redondear(velocidad) + "tt " + tiempo);

velocidad *= 1.12;

radio = radio * 0.65;

k--;
}

velocidad = 2.0 * velocidad * Math.pow(1.0 + radio, 2.0) ;

System.out.println("ntVelocidad disparo : " + redondear(velocidad));
System.out.println("nttiempo total : " + tiempoAcum);

System.out.print("nntseguir(1)/salir(0) : "

;
seguir = Integer.parseInt(in.readLine());

} while (seguir == 1);

bajate el archivo: http://pjsml.50megs.com/java/fuentes/Anillo.java